塔雷伯的警告：停損機制的數學陷阱與風險變形

停損不一定能降低風險，有許多的隱藏問題，可能是你還不知道的。

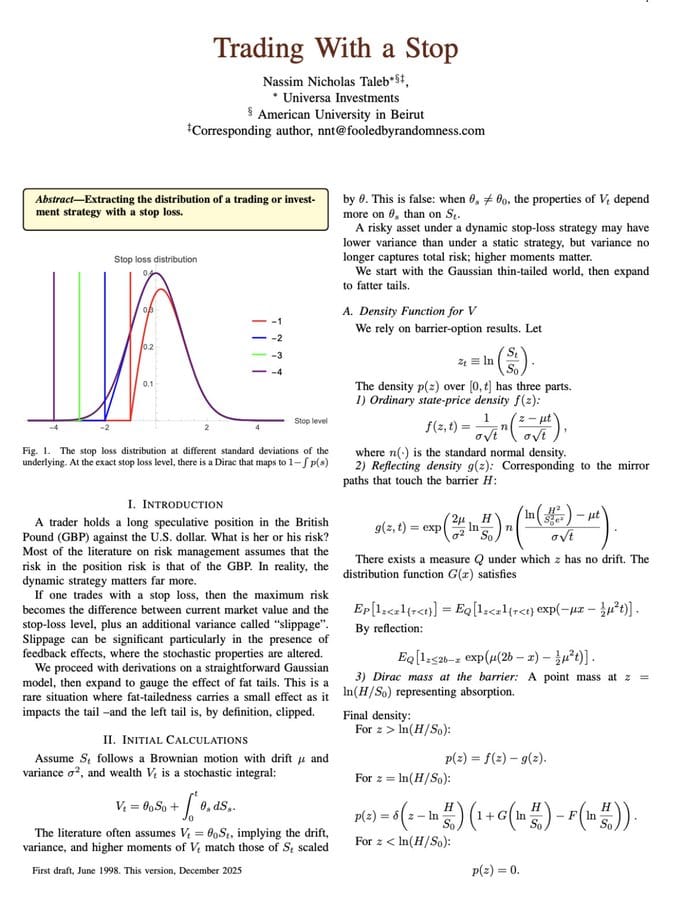
塔雷伯（Nassim Nicholas Taleb，《黑天鵝》與《反脆弱》的作者）最近在 X 上分享了他的新論文《Trading With a Stop》的第一頁，引發金融圈高度關注。

他提出了一個反直覺的論斷：「停損」並不是投資人以為的降低風險萬靈丹，甚至可能會因此創造新的風險。

先說重點，他不是鼓勵大家凹單，也不是說不要停損。而是說，傳統的靜態停損策略可能會改變你的交易策略特性，而這個改變未必是好的。

停損為何不是你以為的保護機制？

多數投資人都相信：只要設定了停損，就能限制最大虧損。

例如在沒有停損的情況下，一個部位的虧損有很多可能：虧 5%、10%、20%，甚至 80%。

然而如果設定了 5% 的停損價格，最多就只會虧損 5%，這可以很直觀的理解，對吧？

但 Taleb 問道，這真的是一個好方法嗎？

滑價問題會讓你虧更多

先從最簡單的部分開始：滑價（Slippage）。

在理想的統計模型裡，這些報酬率會以自然且分散的機率分布呈現，像一片平滑的沙灘。

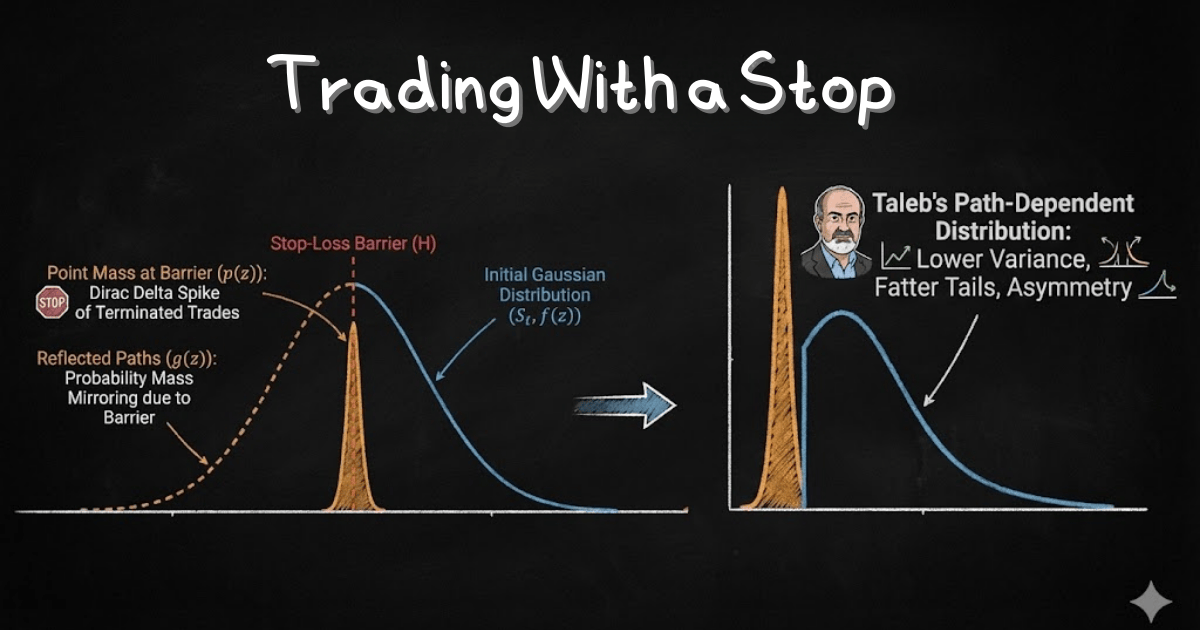
然而，當投資人設定了停損後（例如 -5%），那些原本可能發生在 -10%、-20%、甚至 -80% 的結果，不會真正消失，而是被集中壓縮在 -5% 的那個單一點位。

Taleb 用物理學的概念形容這種現象：「狄拉克質量（Dirac Mass）」—— 一個原本平滑的分布，被尖銳地擠壓成一個高度集中的尖峰、一道牆。

理想 vs 現實

理想狀況：當價格觸及你的停損點 95 元，你的單子會精準地在 95 元成交，實現 -5% 的虧損。

現實狀況：當市場恐慌時（黑天鵝事件），價格不是平滑移動的，而是跳空（Gap）的。

你的停損單掛在 95 元，但市場開盤可能直接跳到 85 元。你的停損單變成市價單，在 85 元成交。預期的 -5% 變成了 -15%。

這就是論文開頭特別強調的：

"Slippage can be significant particularly in the presence of feedback effects, where the stochastic properties are altered."

當所有人都想擠同一個出口時，流動性會瞬間蒸發。價格會直接「跳空」穿過你的停損點。

真實案例

• 2015 年瑞郎脫鉤事件：瑞士央行突然宣布取消瑞郎與歐元掛鉤，EUR/CHF 瞬間暴跌 30%。無數設在 1.20 的停損單，最終在 0.85-0.95 之間成交。
• 2010 年閃崩（Flash Crash）：道瓊指數在幾分鐘內暴跌近 1000 點，許多停損單在極端價格觸發。

這個時候的滑價，就會讓你的虧損比預期的停損點更多，所以不是你設定 -5%，就只會虧損 5% 而已。

路徑依賴：走鋼絲 vs 坐飛機

路徑依賴問題會讓我們的實際報酬率，不是由最終價格來做決定，而是還要考慮我們在持有期間，價格有沒有觸及過停損點做決定。

打個比方：

• 靜態持有像坐飛機：只在乎起飛和降落，中間怎麼顛簸都沒差
• 帶停損交易像走鋼絲：哪怕終點是安全的，只要中間有一秒踩空（觸碰停損），你就掉下去了

實例：川普關稅衝擊

就像是 2025 年四月時的川普關稅衝擊。

中間暴跌了好幾天，但幾個月後已經回到原本價格，到了年底甚至已經漲了兩位數報酬。

但是，每個人都有機會賺到這段報酬嗎？很顯然不是。

如果你在四月份設定了 10% 或 20% 的停損，那麼你可能就會因為觸及停損而出場。後面怎麼漲跌，都跟你沒有關係，即便價格已經回到當時水準，甚至超過許多都是一樣。

這就是市場常說的：價位不變，倉位不見。

你不只失去虧損，也失去了翻盤機會

更大的問題是：你不只失去虧損，也失去了翻盤機會。

在論文的數學推導中，Taleb 指出停損後的概率密度函數會變成：

p(z) = f(z) - g(z) + Dirac Mass

其中：

• f(z) = 原始的價格分布（高斯分布）
• g(z) = 反射密度（Reflecting Density）—— 那些觸及停損障礙後「本來會反彈」的路徑
• Dirac Mass = 在停損點形成的機率尖峰

關鍵洞察：g(z) 不只出現在左邊（虧損區），右邊（盈利區）也會被減掉！

為什麼？因為圖形上右邊的高度變小了，這是因為整個機率分配中，要考慮停損的路徑，所以抵達高報酬的機率降低了。

那些「先虧 10% 再反彈暴賺」的路徑，在設定停損時直接被抬出場，沒機會貢獻盈利了。

數學上的表現就是：獲利區域的機率分佈也會縮水。

變異數的假象：數字會騙人

這裡有個很多人會掉進去的陷阱，也是 Taleb 論文開頭就警告的：

"A risky asset under a dynamic stop-loss strategy may have lower variance than under a static strategy, but variance no longer captures total risk; higher moments matter."

為什麼變異數會變小？

因為停損切掉了左邊的極端虧損，計算出來的變異數（波動率）通常會變小。

沒有停損：

• 可能的報酬：-80%, -50%, -20%, -10%, 0%, +10%, +20%, +50%
• 極端值拉大了整體離散程度
• 變異數 = 大

有 5% 停損：

• 可能的報酬：-5%, -5%, -5%, -5%, 0%, +10%, +20%, +40%（右邊也縮水了）
• 數據點更集中
• 變異數 = 小

很多風控模型看到變異數變小，覺得策略變安全了。

並不完全是這樣的。

風險沒消失，只是結構改變了

現在的風險不再是「波動」，而是那個高聳的「Dirac Mass」（投資人可能會因為停損機制而頻繁被掃地出局）。

形象化理解：

把「偶爾一次大虧 20%」變成了「十次小虧 5%」，表面上穩定了（變異數更小），但總損失可能更大，而且可能錯過反彈機會。

這就是為什麼 Taleb 說：「變異數不再能代表總風險，要看更高階的統計量（峰度 Kurtosis）。」

市場共識的流動性黑洞

除了個人影響之外，Taleb 進一步指出，這些停損點並非孤立存在，而是與其他投資人的停損點一起，在市場上堆積成一個巨大而脆弱的「流動性牆」。

集體行為的自我實現

例如大家常用的：

• 高點回測 5%~10%
• 整數關卡（10000點、20000點）
• 各種均線匯集處（50MA、200MA）

這些位置會有異常高的機率密度，都堆積在同一個點，變成一個脆弱、顯眼、人人都看得到的風險集中區。

市場價格自然會被吸過去，因為那裡正堆著大量等待被觸發的訂單。

為什麼總是「精準打到」你的停損？

這就是為什麼市場常常會精準地「打到」投資者的止損點後才開始反轉——因為所有人都把止損放在差不多的位置，集體造成了流動性黑洞。

而當這個黑洞的流動性被吸收完，市場就會開始反彈，但你的部位已經不見了。

這不是陰謀論，是集體行為的自我實現。

停損機制是一種交換

這表示，我們不需要設定停損嗎？

其實還真不用——如果是指數化的被動投資，基本上不太需要考慮這個。

但如果是主動投資，交易員就需要重新思考這個問題。

交換的本質

Taleb 強調：停損不是降低風險，而是把風險重新分配成另一種形狀。你透過停損，換來的是：

• 高機率的小虧損（頻繁被停損出場）
• 避免低機率但極端的大虧損（崩盤、跳空）

這是一種「以空間換時間」的契約。

你犧牲了「扛單翻盤」的可能性，也就是右邊的獲利區域變低了，並將無限的尾部風險壓縮成了一個高頻的固定損失。

這是一種交換，而不是免費的午餐。

給投資者的啟示

塔雷伯目前只公布了論文的第一頁，裡面有許多數學函數，我就不貼出來了。上面的內容也是自行解讀，可能不完全是作者本人的想法。

X 上有用戶留言說：「你能用五歲小孩都能聽懂的方式解釋一下嗎？」

塔雷伯回應：「五歲小孩不用進行交易。離開市場吧。」

真的是有夠嗆～

不過我覺得這個題目真的很有趣，後續有更多內容與結論再來跟進。

而從過去經驗，塔雷伯的數學跟交易哲學，通常是可以連結到人生處世法則的。

以這個理論來看，或許是在提醒我們：

「看似安全的保護機制，其實反而可能讓你不斷挫敗，甚至失去翻盤的機會。」

例如，遇到挫折就立刻放棄、失敗一次就轉換工作跑道，表面上是「保護自己不受更大傷害」，實際上卻錯過了「谷底反彈」的可能性。

就像川普關稅那段時間，如果在四月恐慌時出場，就看不到年底的豐厚報酬。

人生也是如此。有時候，真正的成長來自於「扛過低谷後的反彈」，而不是「每次遇到困難就停損離場」。推薦去看看黃仁勳的創業過程。

當然，這不是要鼓勵大家無腦硬扛，而是要認清：

每一個「保護機制」都有代價，而不是免費的午餐。

不管是投資，或是人生，都是如此。

結語

Taleb 的這篇論文提醒我們：

1. 停損不是保險，是交換：用高頻小虧換取避免極端大虧
2. 變異數變小是假象：風險沒消失，只是結構改變了
3. 你會失去翻盤機會：獲利區的概率分佈也會縮水
4. 流動性黑洞：集體停損行為會自我實現

在風險管理的世界裡，沒有零成本的保護。
理解你真正承擔的是什麼，才是投資中最關鍵的安全措施。

參考資料

• Nassim Nicholas Taleb: Trading With a Stop (December 2025)
• 論文涉及概念：Dirac Mass、Reflection Principle、Path Dependence、Barrier Options
• 相關研究：布朗運動（Brownian Motion）、隨機微積分（Stochastic Calculus）